START-PROF automatically takes into account the following effects associated with internal pressure in the piping:

Unrestrained pipe elongation of pipe from pressure consists of two parts. First part is elongation due to pressure load on end cap. The second part is pipe shortening due to Hook’s law.
Pipe elongation prom pressure load on end cap is:
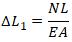
L – Pipe Length
E – Modulus of Elasticity
Pipe cross-section area is
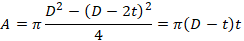
D – Pipe Outer Diameter
t – Pipe Wall Thickness
N – Axial Force in the Pipe
Axial force is equal to the force acting on cap
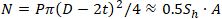
P – Internal Pressure
Pipe elongation will be
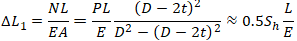
Sh – Hoop Stress in the Pipe
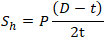
According to Hooke's law the axial deformation of the pipe under axial stress is:
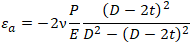
v – Poisson’s Ratio
Pipe shortening due to internal pressure:
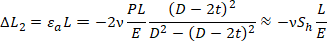
Total pipe elongation from pressure load is
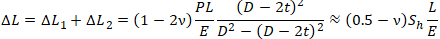
If we add thermal expansion elongation the equation will be:
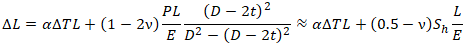
DT – Temperature Difference between Installation and Operation temperature
a – Coefficient of thermal expansion
Longitudinal stress caused by internal pressure is
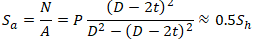
Some codes use following strength criterion for unrestrained pipe:
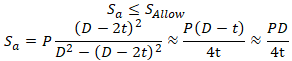
If we add here bending stress M/Z and axial stress N/A from loads other than pressure, we get
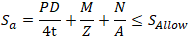
If we want to add torsion stress, we should calculate equivalent stress:
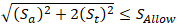
Sallow - Allowable stress
Thermal expansion has no effect on unrestrained piping systems, i.e. this equation usually used for sustained and occasional stress check in piping systems from pressure, weight and other force-based loads.
The code equations were created for manual calculation. But now most of pipe stress analysis software can consider Bourdon effect. This means that code equations should be modified to match the current level of technology.
Axial force N in START-PROF is always calculated considering Bourdon effect, thus we should subtract (PD/4t)A value from axial force otherwise it will be included twice:
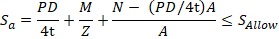
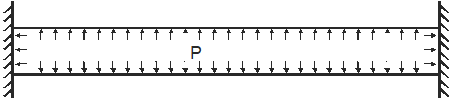
For a restrained pipe with two anchors on both ends, thermal and pressure expansion should be zero
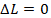
The axial force required to compress the pipe back to its original length can be calculated from this equation:
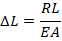
Therefore support load should be:
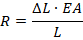
After substitution the DL equation we got final support load for restrained pipe. In literature, the R value also called as "Effective Axial Force":
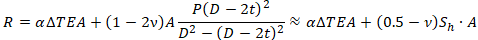
The value of axial force can be obtained from the equilibrium conditions near the anchor. Axial force is equal to reaction in anchor subtract the pressure thrust force that is received by anchor and doesn’t acting on the pipe:
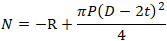
Final equation for axial force in restrained pipe is

Axial stress in the restrained pipe will be
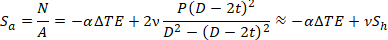
A strength criterion for totally restrained pipe is:
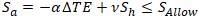
If we add here bending stress M/Z and axial stress N/A from loads other than pressure, we get
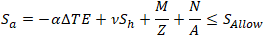
If we want also consider torsion and hoop stress, we should use the equivalent stress equations like described for unrestraint pipes.
If axial force N is calculated using software that considers Bourdon effect, then we should subtract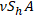 value:
value:
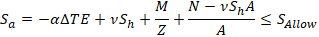
If we add flexible spring instead of rigid anchor on the right end of the pipe, we will get the third pipe condition – partially restrained.
We will pass the derivation of equations process and just show the final equations in table below. The "support load" equation also called in the literature as "Effective axial force". Please see the next paragraph for the explanation.
The strength criteria for partially restrained pipes should be from sustained primary loads:
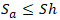
From occasional primary loads
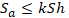
From both primary and secondary loads acting simultaneously
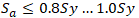
Primary - are force driven not self-limiting loads like weight, pressure, relief valve thrust, wind, etc.
Secondary – are displacement driven self-limiting loads like thermal expansion, anchor movements, support or soil settlement, etc.
Unrestrained and fully restrained pipe conditions can be easily calculated manually, but third condition require using of pipe stress analysis software, because spring stiffness k depends on connected pipes.
The "Support Load, R" equations from the table above also called in the literature as an "Effective Axial Force". And "Axial Force, N" called as the "True Axial Force".
The "True Axial Force" ("Axial Force" in the table above) is used for:
Axial pipe stress calculation. It can be found in Code Stress Table in PASS/START-PROF
Local pipe wall buckling analysis. It can be found in the Pipe Wall Buckling Table in PASS/START-PROF
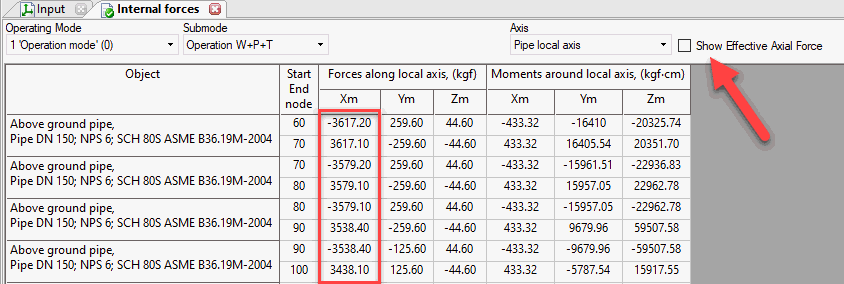
Pipe element internal forces. It can be found in the Internal Forces in Piping Elements Table in PASS/START-PROF. The check box "Nozzle Loads" should be unchecked
The "Effective Axial Force" ("Axial Force" in the table above) is used for:
Loads on the support calculation. It can be found in Loads on Supports and Restraints Table in PASS/START-PROF
Loads on Pressure Vessel and Tank Nozzles, Rotating Equipment Loads etc. It can be found in Loads on Nozzles and Equipment Table in PASS/START-PROF
Flange Leakage Check. It can be found in the Flange Leakage Check Table in PASS/START-PROF
Pipeline upheaval buckling calculation. It can be found in START-Elements for straight buried pipe and for buried long-radius bend
Pipeline global buckling (Euler buckling) calculation. It can be found in START-Elements
Pipe element internal forces. It can be found in the Internal Forces Table in PASS/START-PROF. The check box "Nozzle Loads" should be checked
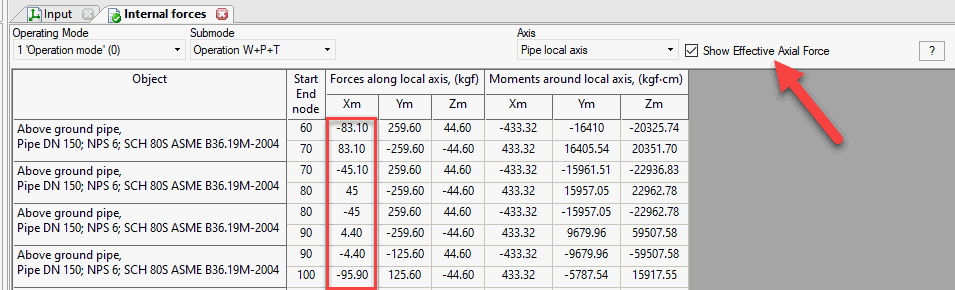
Why the "Effective Axial Force" should be used to calculate the nozzle loads, flange check, global buckling instead of the "True Axial Force"?
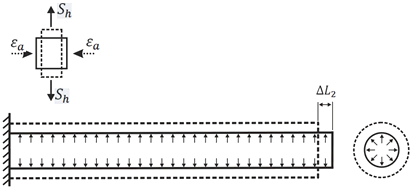
If the left end of the pipe on the picture below is connected to pressure vessel nozzle or rotary equipment, then the "true" axial force in the equipment nozzle will be N (see table above). But when equipment manufacturers calculate allowable loads using finite element software like PASS/NOZZLE-FEM, they assume that nozzle has the end cap and vessel is under pressure. This means that axial stress caused by pressure thrust is already taken account when nozzle allowable loads was calculated and should not be considered twice.
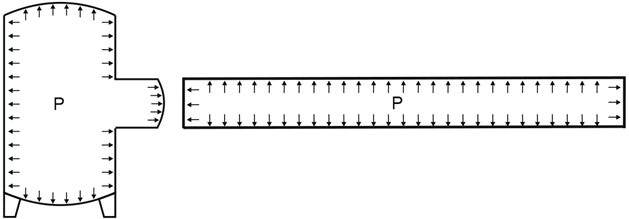
Hence we must exclude the pressure thrust load from the True Axial Force and use this value to compare with the nozzle allowable loads. This means that we must use the Effective Axial Force for equipment nozzle checks. For example if we connect a pipe with the end cap to the nozzle, the true True Axial Force in the nozzle wall will be
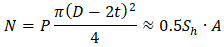 '
'
but we should exclude the pressure thrust component from this force i.e. use the Effective Axial Force that equals to zero. We can imagine it if imagine that nozzle and the pipe both has the end caps like on the picture above. Therefore the nozzle load will be zero.
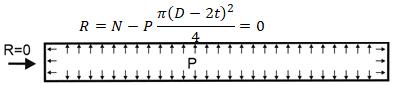
The same explanation can be offered for the flange leakage check. If you look at the equivalent pressure method equation, you will see, that the internal pressure is already taken into account and we should apply only additional loads, caused by thermal expansion and other influences, but not by pressure the thrust.
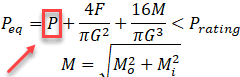
But why we should use the "Effective Axial Force" for global buckling and for upheaval buckling calculation, but but at the same time using the "True Axial Force" for local pipe wall buckling? This phenomena a little bit harder to explain. I will try to do it using the simple examples.
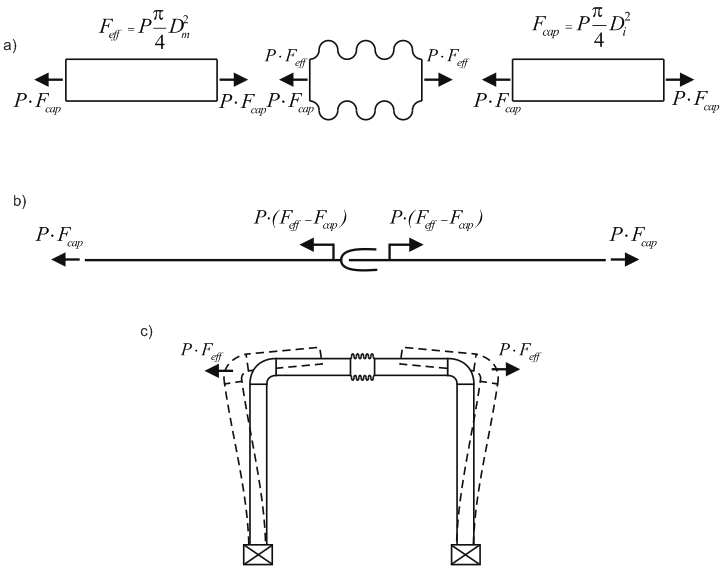
To calculate the longitudinal buckling we need to consider the deflected pipe shape, not the initial (installation) shape. To explain this effect, let's look at this simple model, consisting of the two pipes (a). The "cap pressure" forces acting on the pipe ends P·A as a result of summing the vectors produce the force "S" that tends to push the pipe in lateral direction. If we represent the pipe as a polygonal chain (b), then at the each turn of the pipe we will have a lateral force "S" trying to push the pipe away. And finally if we will represent the pipe as the infinite number of polygons, we will have a uniform lateral load "S" that leads to pipeline global buckling.
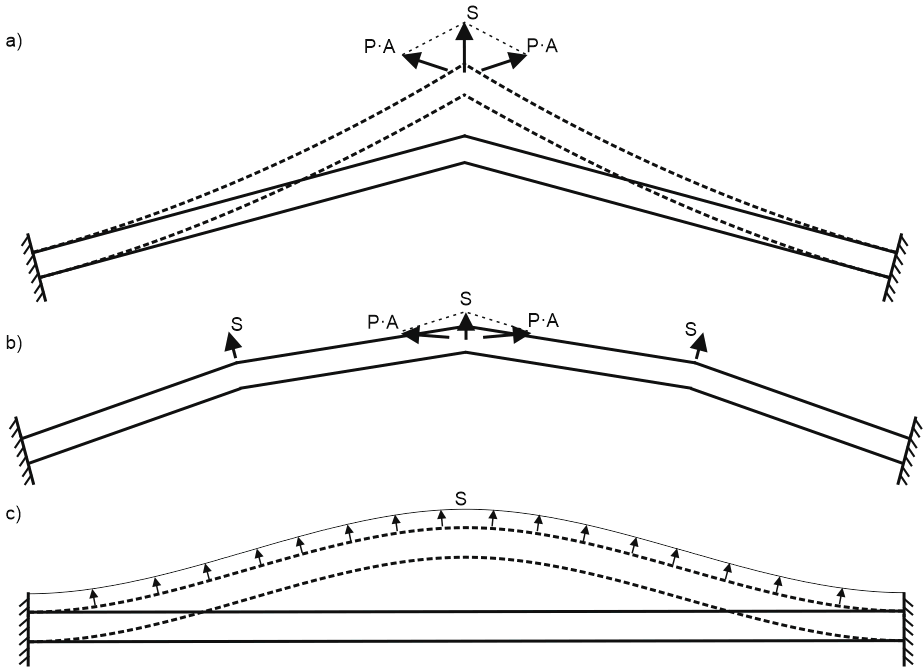
I will pass the derivation of equations process, you can find it in the literature and just say that the final conclusion is that the effective axial force "R" should be compared with the critical axial force value. For elastic buckling and without the soil resistance the Euler's equation will be:
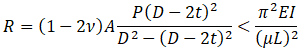
Not the true axial force "N". The additional "cap pressure" force generate the distributed load "S". Also this phenomena can be explained by the fact, the in the deflected form the outer pipe wall length is longer than the internal wall length, hence the total pressure force on the outer surface is greater by "S" value.
Also, the next analogy helps to understand this phenomena. Imagine the restrained pipe under the pressure just like the reinforced concrete beam. The pipe is playing the role of the reinforcing bar (stretched) and the pipe content (water) buckling happens just like of the compressed rod (see the picture below).

PASS/START-PROF software considers pressure Bourdon effect in arbitrary piping model. START-PROF model the pressure loads consist of two parts.
Firstly, START-PROF adds pressure thrust force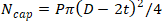 on
each end of the pipe.
on
each end of the pipe.
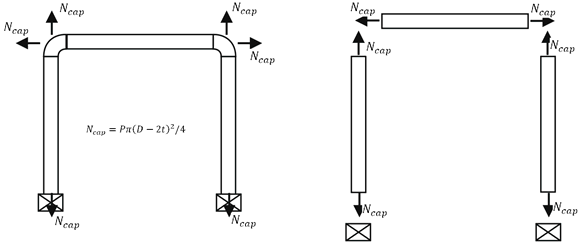
Secondly, START-PROF adds axial deformation for each pipe. It equal to pipe thermal elongation minus pressure shortening, also known as Bourdon effect. Pipe total axial expansion will be
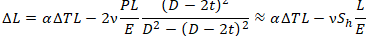
The combination of these two loads allows correct modeling any type of piping: unrestrained, restrained, and partially restrained.
Bourdon effect makes a significant contribution to the support loads, displacements, and stresses forSTART-PROF always preforms analysis with Bourdon effect.
Internal pressure creates unbalanced forces acting on caps and convolutions of bellows (a), causing stretch in unrestrained pipelines (b). If the piping is restrained between supports, it cannot expand and passes thrust force onto supports (c).
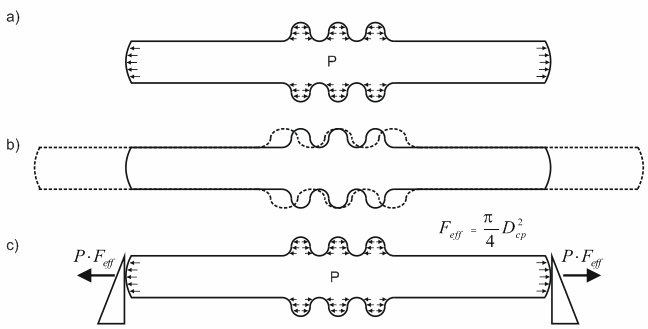
Fig. 3. Thrust force passed onto supports in pipelines with axial expansion joints
Thrust force passed onto supports in a straight pipe ("cap pressure") is equal to
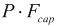
Thrust force passed onto supports in a not pressure balanced axial expansion joint is equal to
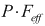

Thrust force passed onto supports in a pressure balanced axial expansion joint is equal to 0
START-PROF axial expansion joint model is shown in following figure. Pipe pressure balances part of thrust force in a not pressure balanced axial expansion joint; therefore, during analysis loads equal to the thrust force difference for the pipe and axial expansion joint are applied to nodes on either side of the axial expansion joint.
a - Thrust force in piping with axial expansion joint, b - START-PROF model,
c - Thrust force from expansion joint acts on anchors
Bourdon effect is the straightening of a bend with initial ovalization due to internal pressure. This affects resulting displacements and loads on supports. Bourdon effect appears only when the ovalization factor is a > 0.
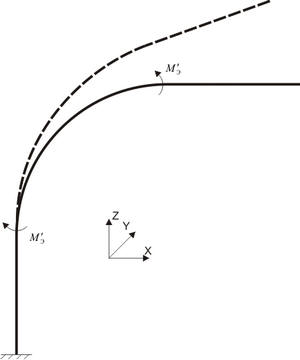
To model Bourdon effect, bending moments Mэ acting in the bend plane are automatically applied to bends. Their value is calculated based on formulas deduced according to [1] and [2]:
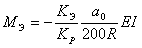 ,
,
where
a0 - ovalization factor, %
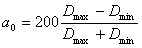
Кp - bend yield factor,
Kэ - factor describing the effect of cross-section ellipticity on bend axis skewing,
R - bend axis radius.
1. Kostovetsky D.L. Pipe stress of power piping. St. Petersburg, 1973
2. Zverkov V.B., Kostovetsky D.L., Kats Sh.N., Boyaji K.I. Pipe stress analysis handbook. St. Petersburg, 1979