
Read about START-PROF pipe stress analysis software
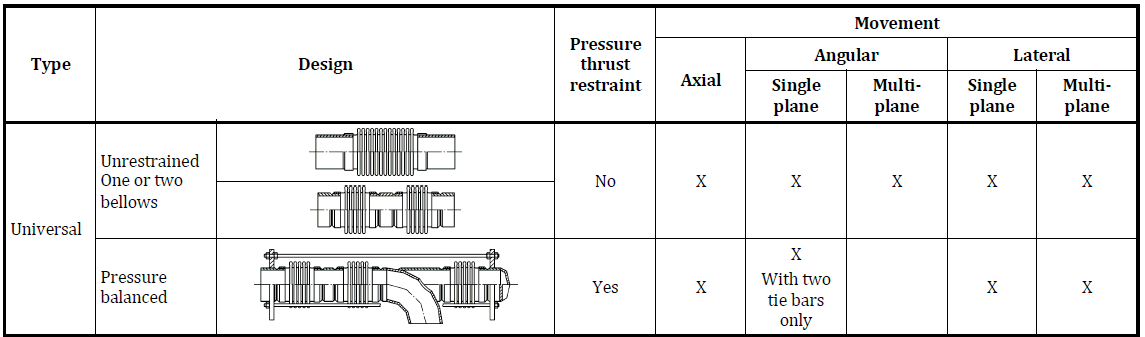
Universal Expansion Joints are simple bellows without tie rods (untied). It can be exposed for bending, compressing, tension, lateral, and torsion deformations.

All expansion joint properties can be taken from expansion joints database by pressing the "..." button and selecting the appropriate expansion joint.
Expansion Joint analysis results can be found in Expansion Joint Deformation Table. See also "How to Reduce the Nozzle Loads in START-PROF"
Universal expansion joints may have one or two bellows and also can be pressure balanced.
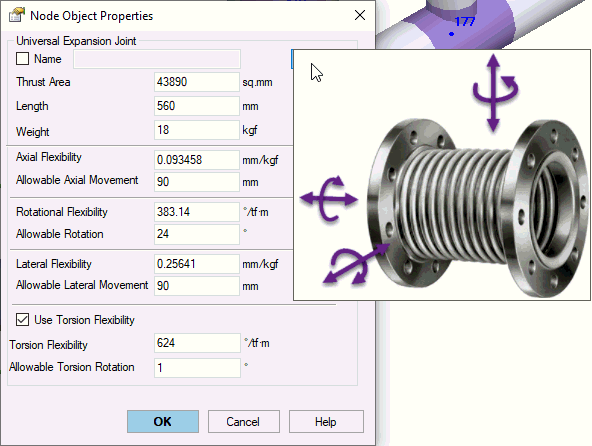
Property |
Description |
Name |
Element name. If checked then it shown in 3D view |
Effective area1 |
Expansion joint effective area. Used for calculating thrust force. More.. For bellows, Effective Area Aeff is an area if circle with an Effective mean bellows diameter Deff: Aeff = Pi * (Deff)^2 / 4 Approximately Deff = (Dmin + Dmax)/2 is mean bellows diameter. Value must be obtained from manufacturer For pressure balanced expansion joints Aeff=0. |
Length |
Expansion joint length Lu. In the internal second layer hidden model PASS/START-PROF model this type of expansion joint as zero length expansion joint and adds two rigid elements with length Lu/2 on the both sides. Non zero-length expansion joints can be modeled using Flexible Element |
Weight |
Expansion joint weight that is applied on the rigid elements (half on the left and half on the right) |
Axial Flexibility1 |
Axial flexibility, (1/Kax) of whole length of expansion joint (all convolutions). Kax = Axial stiffness of the bellows. Value must be obtained from manufacturer |
Axial Allowable Deformation, Δk1 |
Allowable axial expansion movement (maximum allowable linear deformation): Δk/2, where Δk - full allowable axial expansion movement. Used for analyzing expansion joint deformation. Value must be obtained from manufacturer |
Rotational Flexibility1 |
Rotational flexibility, (1/Kb) of whole length of expansion joint (all convolutions). Kb - Bending angular stiffness. value must be obtained from manufacturer. No need to multiply it by 4, because expansion joint is modeled as zero length. Bending angular stiffness can be calculated by EJMA equation: Kb = Kax·Deff²/8, Kax = Axial stiffness of the bellows Deff = Effective diameter mean diameter of the bellows |
Allowable Rotation1 |
Allowable rotation angle - maximum allowable rotational deformation. Value used for expansion joint deformation analysis. Value must be obtained from manufacturer |
Lateral Flexibility1 |
Transverse lateral flexibility, (1/Ktr) of whole length of expansion joint (all convolutions). Ktr - Transverse lateral stiffness. Value must be obtained from manufacturer Transverse lateral stiffness can be calculated by EJMA equation: Ktr = 1.5·Kax·(Deff/L)², Kax = Axial stiffness of the bellows Deff = Effective diameter mean diameter of the bellows L = Length of the bellows for all convolutions |
Allowable Lateral Deformation1 |
Allowable lateral expansion movement - maximum allowable transverse linear deformation. Value used for expansion joint deformation analysis. |
Note 1: Thrust area, flexibility and allowable axial expansion movement can be taken from expansion joints database by pressing the "..." button and selecting the appropriate expansion joint.
After analysis the relative displacements of flexible joint are checked by equation:

If allowable torsion rotation available, then 4th member is added to the equation above