Node deformation is the mutual displacement of adjoining pipe cross-sections. It is used, for example, for modeling expansion joint pre-stretch.
For more information, see load combination.
Node deformation can be input for any point along a straight pipe, except where supports or restraints are placed. In rare cases where node deformation must be input in a node where a support is installed, a new node should be created at a very short distance from the support (e.g., 1mm) to input the necessary effects.
Node deformation can be of the following types:
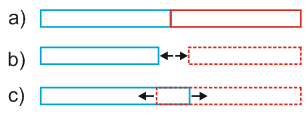
Pre-compression (Cold Push) (fig. 1.b). This is a special case of linear deformation and can model pre-compression.
Cold spring (Cut Short, Cold Pull) (fig. 1.c). This is a special case of linear end displacement and can model pre-stretch.
Linear and rotational deformation in node. Linear mutual adjoining pipe end displacement in any direction (fig. 2, 3)

a - initial condition, b - compression of pipes, c - tension of pipes
Fig. 1. Linear stretch and compression along the pipe axis
Pre-stretch can be viewed as: in a closed circuit piping model, a pipe section of a certain length is cut out in a node and pipe ends are forced toward each other and welded. Stretch force is created in elements adjoining the node. Pre-compression is the reverse - an additional pipe element of a certain length is inserted in a node, creating compression force in adjoining elements.
Stretch and compression deformation is always input along the local element axis Xm.
Linear and rotational displacement of adjoining pipe ends are input as projections on the global coordinate axes, where direction must be indicated with negative or positive signs. Direction is input in the global coordinate system used in START-PROF.
Note that not absolute, but relative displacement is input - i.e., displacement of one pipe end relative to the other. The node of the element relative to which displacement is input must be indicated.
For example, fig. 2.b shows linear displacement of element BC relative to element AB. In this case, node A should be indicated. Fig. 2.c shows linear displacement of element AB relative to element BC. In this case, node C should be indicated. In other words, the element to which the indicated node belongs remains stationary, while the second eloement is displaced by a distance of ΔX, ΔY, ΔZ. Fig. 2 shows that the same ΔX, ΔY, ΔZ values produce different deformation properties.
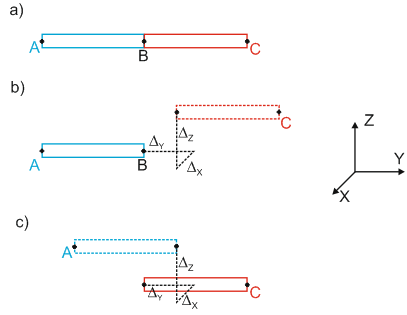
a - initial condition, b - linear displacement relative to node А, c - linear displacement relative to node С
Fig. 2. Mutual linear pipe end displacement
The above also applies for rotational displacement (fig. 3.b and c).
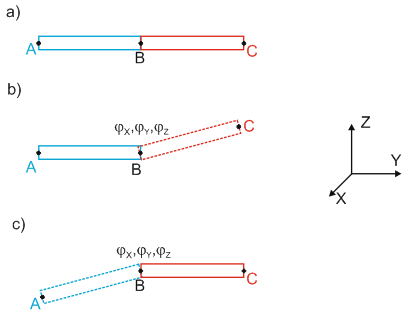
a - initial condition, b - Angular displacement relative to node А, c - Angular displacement relative to node С
Fig. 2. Mutual linear pipe end displacement
Fig. 3. Mutual rotational pipe end displacement
Insert > Displacement > Cold Spring (Cold Push)
Insert > Deformation > Cold Spring(Cold Pull)
Insert > Deformation > Move and Rotate Restraint
Insert > Deformation > Relative Displacement in the Node