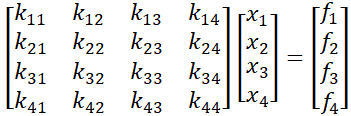
Set the Project Settings
Create the Piping Model in 3D view window
Analyze results in errors and warnings window, output reports, output 3D window
Stress analysis is used for selecting the main Piping dimensions and placing supports. Pipe and fitting wall thickness must follow codes of standards.
The Piping is considered as an elastic beam system. Flexibility factors for bends, miter joints, single miter joint and tee branches is taken into account, as well as displacement deformation for pipes. The Piping is divided into straight and bent elements. Element connection points are called nodes. Nodes are inserted in the following cases:
at attached locations for vessels, equipment, containers, manifolds, etc.;
at support placement locations;
at Piping axis direction change or in tees;
at points of soil or pipe property changes (pressure, wall thickness, etc.).
Non-linear effects are considered, caused by:
friction in supports
friction in torsion joint, ball joint, slip joint
single-directional restraints (lift off supports)
Gaps
Pipeline and soil interaction in buried elements
If necessary, START-PROF can:
automatically select variable spring support springs based on published methods [4].
analysis of strength and carrying capacity for the Piping and connective fittings based on standards
During the analysis of buried pipelines, soil is represented by the correlation of the soil resistance to displacement, where this correlation is determined by the direction of displacement of the pipeline in relation to soil surface. The correlation of soil resistance to displacement is nonlinear. START-PROF's soil model is based on published experimental and theoretical data [2,3]. Soil is a continuous base, modeled by discrete nonlinear variable spring supports placed along the pipeline, the flexibility of which is determined by the value and direction of displacements. START-PROF uses Ainbinder's algorithm. Each nonlinear variable spring support consists of three restraints: vertical, horizontal (perpendicular to the pipeline axis) and longitudinal (along the pipeline axis). Iteration finishes when displacements in the direction of restraints stop changing. The distance between supports is determined automatically.
START-PROF analysis follows the following structure:
Input data logic check for errors and warnings. If present, an error or warning message will be displayed.
Check of all Piping elements for pressure. For all Russian codes: if any one of the Piping elements does not pass for design or test pressure, an error message will be displayed and the analysis will be halted.
Spring selection
A number of analyses based on structural mechanics methods and taking into account various non-linear effects on various load and force combinations
Stress calculation and spring strength conditions selection based on properties set in standards
Display of notes about issues in the output
START-PROF uses structural mechanics methods for beam structures, see [5], [6] and similar literature. The piping system is considered as consisting of straight and curved beams. Straight beams are pipes, rigid elements and valves, while curved beams are the bends.
Traditional stress analysis software usually using the direct stiffness method K*X=F [5], [6]
K - element stiffness matrix
X - displacement vector (unknowns)
F - load vector
For 4 degree of freedom system (DOF) it will be:
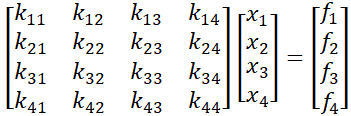
The main disadvantage is high memory usage and low calculation speed for the big models. Advantage is very easy and transparent algorithms for programming.
In the stiffness method, displacements X (rather than forces) are taken as the unknown quantities. For this reason, the method is also called the displacement method. The unknown displacements X are obtained by solving equations of equilibrium (rather than equations of compatibility) that contain coefficients in the form of stiffnesses K.
The flexibility method A*R=D [5], [6].
A - element flexibility matrix
R - load vector (unknowns)
D - displacement vector
For 4 degree of freedom system (DOF) it will be:
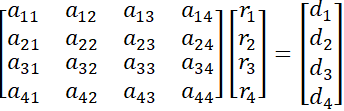
The flexibility method advantage is that this method for tree-like systems like piping gives a several times less unknowns than stiffness method. The matrix is several times smaller. And solution time several times faster and require less memory. The main disadvantage of flexibility method is a very complex algorithms for programming.
The flexibility method is based upon the solution of equilibrium equations and compatibility equations. There will always be as many compatibility equations as redundants. It is called the flexibility method because flexibilities A appear in the equations of compatibility. Another name for the method is the force method because forces F are the unknown quantities in equations of compatibility.
PASS/START-PROF uses the combined flexibility and stiffness method [1]. It use the combined matrix and combined unknowns (displacements in expansion joints and reaction forces in supports). Method uses the equations:
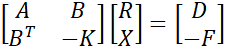
A - element flexibility matrix (displacements caused by unit forces, applied along the direction of unknown forces r)
K - element stiffness matrix (reactions caused by unit displacements, applied along the direction of unknown displacements x)
B - matrix of displacements from unit forces, applied along the direction of unknown displacements x
R - vector of unknown forces
X - vector of unknown displacements in expansion joints and cut-points of piping system
D - vector of applied displacements
F - vector of applied forces
For example we have a 4 node frame (a) with anchors at nodes 1 and 4, hinge in node 2 and applied force at node 3
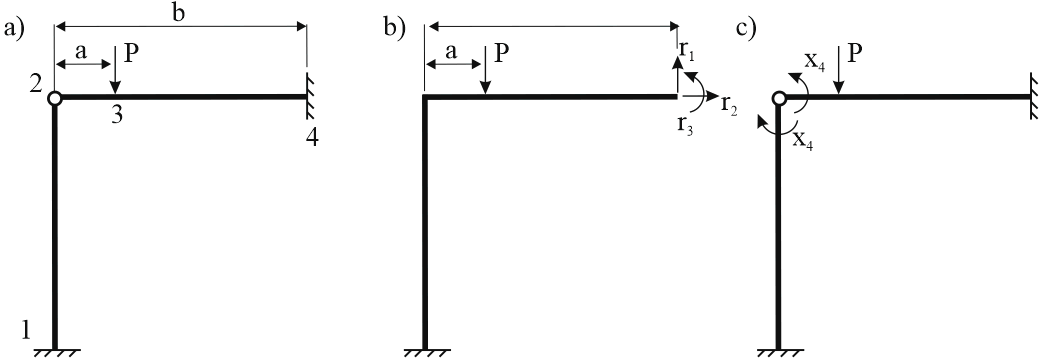
a - frame model, b - primary structure for flexibility method, c - primary structure for stiffness method
The primary system for flexibility method (b) can be obtained by removing the anchor 4 and applying the unknown loads r1, r2, r2. It will be a console system from anchor 1. The node 2 assumed as rigid.
The primary system for stiffness method (c) will be a system with the hinge in node c and unknown displacement x4.
The system of equation to solve this problem will be:
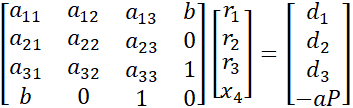
The following equation states, that the moment in hinge should be zero (lowest row of the system of equations):
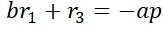
This method has been chosen in 1965 when START-PROF was created, because it is has lowest memory usage and fastest solution time for typical tree-like piping systems. On modern machines it allows to achieve the results of the complex nonlinear piping systems very quickly.
For example we have the following system:
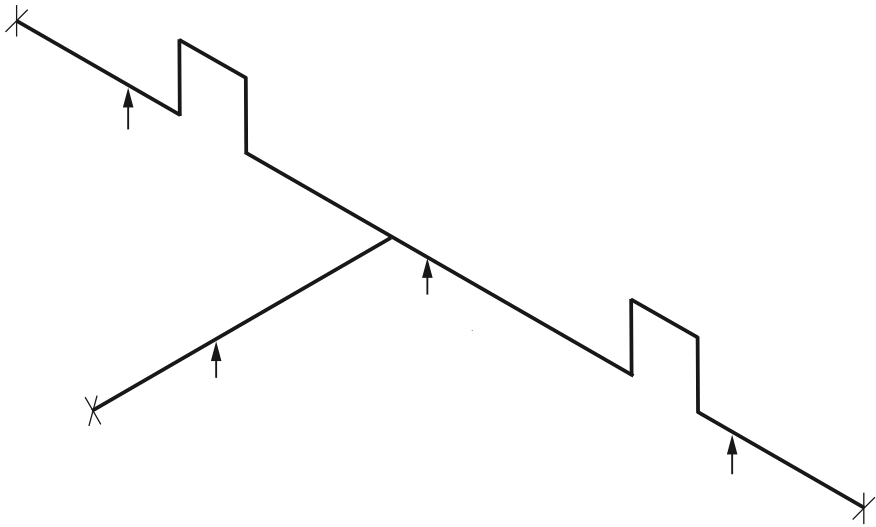
In classical FEM software using stiffness method this system will have 78 unknowns. The matrix K will be 78x78. Consume a lot of memory and need a lot of time for solution.
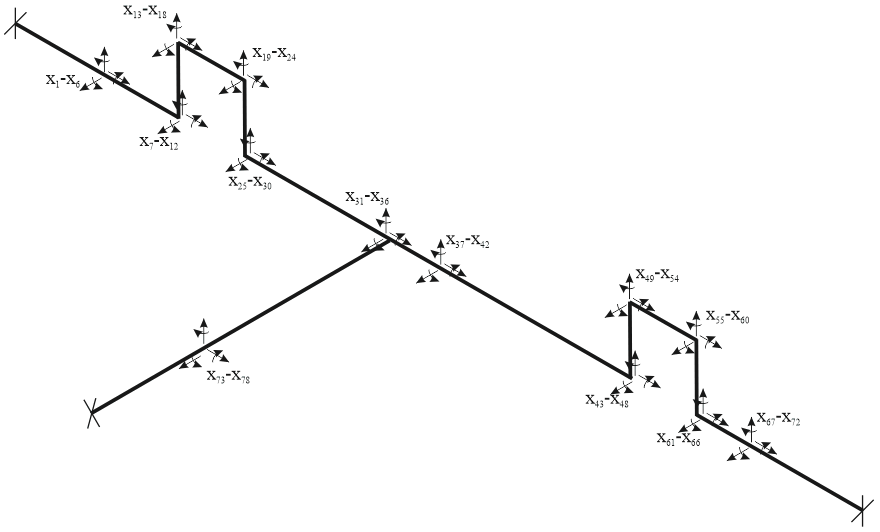
In START-PROF combined flexibility-stiffness method this system will have just 24 unknowns. The matrix will be 24x24 with same analysis results.
The special cut-points A and B will be automatically added that breaks the piping system into 3 parts - "consoles".
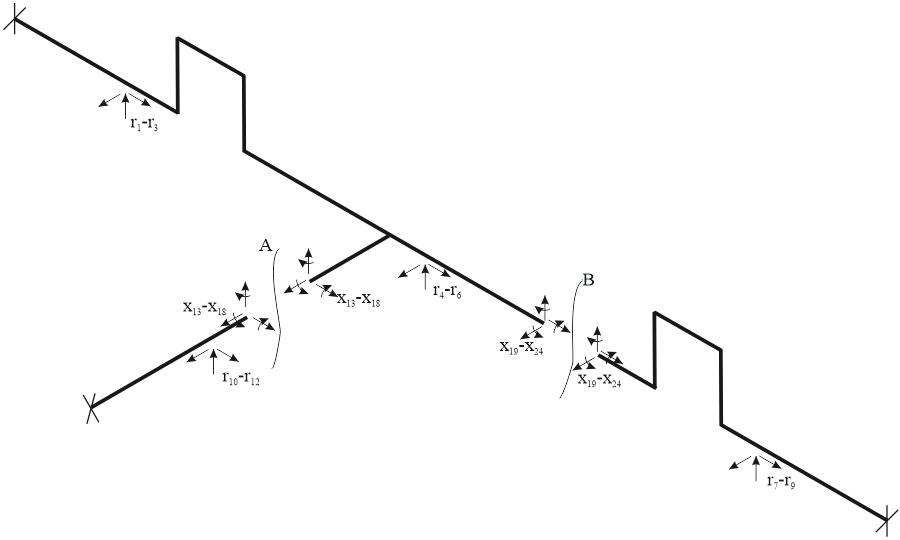
In classical stiffness method the boundary conditions are zero displacements x at the nodes, where we place the supports. If we solve the nonlinear piping system assuming some pre-defined tolerance, the displacements at the support points will be always zeroes.
In flexibility method after matrix solution we obtain the unknown forces r instead of displacements. If we solve the nonlinear piping system assuming some pre-defined tolerance, the support reaction forces r will be obtained with some tolerance. After solution, START-PROF calculates the displacements at all nodes of each console, using the reaction forces r. The displacements will be obtained with some tolerance also. This can cause that some rigid supports will have non zero displacements, for example 0.5 mm. It is not an issue, it is just a solution tolerance. Usually it happening in systems that has a very-very long consoles. It doesn't need any action from user.
But if you want to increase the accuracy of displacements, add the special marker (M) objects. It breaks the long console into several parts. Additional 6 unknown reaction forces x are added at this point and consoles become shorter.

1. Magalif V., Yakobson L. Pipe stress analysis on computers (START-PROF authors). Moscow, 1969
2. Aynbinder A., Kamershtein A. Transmission pipelines stress and stability analysis. Moscow, 1982
3. Skomorovsky Y., Aynbinder A. Longitudinal displacements of buried pipelines considering soil physical nonlinearity, VNIIST, Moscow, 1975
4. Variable spring hanger selection for power and nuclear piping RTM 24.038.12-72, 1973
5. Weaver W., Gere J. Matrix Analysis of Framed Structures
6. Nagarajan P. Matrix methods of structural analysis